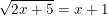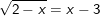Karmila: Desember 2021

1. Jika f(x) = 3x + 2 dan g(x) = 4x2 . Maka (f o g)(x) dan (g o f)(x) adalah …

Pembahasan

(f o g)(x) = f (g(x))

(f o g)(x) = f (4x2)

(f o g)(x) = 3(4x2) + 2

(f o g)(x) = 12x2 + 2

(g o f)(x) = g(f(x))

(g o f)(x) = 4(3x + 2)2

(g o f)(x) = 4(9x2 + 12x + 4)

(g o f)(x) = 36x2 + 48x + 16

Jadi, (f o g)(x) = 12x2 + 2 dan (g o f)(x) = 36x2 + 48x + 16.

2. Diketahui (f o g)(x) = 2x + 4 dan f(x) =x – 2. Tentukan fungsi g (x)!

Pembahasan

(f o g)(x) = 2x + 4

f(g(x)) = 2x + 4

g(x) – 2 = 2x + 4

g(x) = 2x + 4 + 2

g(x) = 2x + 6

Jadi, fungsi g (x) adalah g(x) = 2x + 6.

3. Tentukan f(x) jika (f o g)(x) = 4x + 6 dan g(x) = 2x + 5.

Pembahasan

(f o g)(x) = 4x + 6

f(g(x)) = 4x + 6

f (2x + 5) = 4x + 6

Misal u = 2x + 5, maka x = ½(u-5), sehingga:

f (2x + 5) = 4x + 6

f (u) = 4(½(u-5)) + 6

f (u) = 2u – 10 + 6

f (u) = 2u – 4

f (x) = 2x – 4

Jadi, fungsi f(x) = 2x – 4.

4. Tentukan f⁻¹(x) dari f(x) = 2x + 4

Jawab
Kita gunakan rumus fungsi invers pada baris pertama tabel

f(x) = 2x + 4

f(x) – 4 = 2x

$Rumus Fungsi Invers dan 4 contoh soal 91$

$Rumus Fungsi Invers dan 4 contoh soal 92$

5. Tentukan f⁻¹(x) dari $Rumus Fungsi Invers dan 4 contoh soal 93$

Jawab

Sekarang kita masukan rumus fungsi invers pada baris ke-2 tabel
$Rumus Fungsi Invers dan 4 contoh soal 93$

(7x+3) f(x) = 4x -7

7x f(x) + 3 f(x) = 4x – 7

7x f(x) – 4x = – 3 f(x) – 7

(7 f(x) – 4)x = – 3 f(x) – 7

$Rumus Fungsi Invers dan 4 contoh soal 95$

$Rumus Fungsi Invers dan 4 contoh soal 96$

6. Tentukan f⁻¹(x) dari f(x) = x² – 6x + 15!

Jawab
Sekarang kita masukan rumus fungsi invers pada baris ke-3 tabel

f(x) = x² – 6x + 15

f(x) = x² – 6x + 9 – 9 + 15

f(x) = (x-3)² + 6

f(x) – 6 = (x-3)²

$Rumus Fungsi Invers dan 4 contoh soal 97$

$Rumus Fungsi Invers dan 4 contoh soal 98$

$Rumus Fungsi Invers dan 4 contoh soal 99$

7. Tentukan f⁻¹(x) dari f(x) = eˣ⁺⁷!

Jawab

Kita gunakan rumus fungsi invers pada baris ke-5 tabel
f(x) = eˣ⁺⁷

ᵉlog f(x) = x + 7

x = ᵉlog f(x) – 7
(karena ᵉlog x = ln x)

f⁻¹(x) = ln x – 7

Daftar Pustaka

Athirah.Muthi Zahrani.2021."Rumus Fungsi Invers dan 4 contoh soal"https://www.zenius.net/blog/rumus-fungsi-invers.diakses pada tanggal 14 Desember 2021

Kevin.2021"Contoh Soal Fungsi Komposisi: Jawaban Dan Pembahasannya"https://rumuspintar.com/fungsi-komposisi/contoh-soal/.diakses pada tanggal 2021

1. Tentukan himpunan penyelesaian dari 1/x-3 = 1/4

Jawab:

1/x-3 = 1/4

1×4 = 1 × (x-3)

4 = x-3

4+3 = x

7 = x

2. Tentukan himpunan penyelesaian dari 3x/x+1 = 2/5

Jawab:

3x/x+1 = 2/5

3x × 5 = 2 × (x+1)

15x = 2x+2

15x - 2x = 2

13x = 2

x = 2/13

3. Diketahui persamaan rasional x/x+3 = x+1/x-2 , tentukan nilai x yang memenuhi

Jawab:

x/x=3 = x+1/x-2

x(x-2)= (x+10 (x+3)

x²-2x=x²+3x+x+3

x²-2x=x²+4x+3

x²-x²-2x-4x=3

-6x=3

x= -1/2

4.5x−20x/5≤3

Langkah pertama , kita perlu menjadikan ruas kanan pada pertidaksamaan menjadi nol, yaitu dengan mengurangi kedua ruas dengan

3

, kemudian sederhanakan bentuk pada ruas kiri dengan menyamakan penyebutnya

\begin{aligned} \frac{5 x - 20}{x - 5} - 3 & \leq 3 - 3 \\ \frac{5 x - 20}{x - 5} - 3 & \leq 0 \\ \frac{5 x - 20}{x - 5} - \frac{3 (x - 5)}{x - 5} & \leq 0 \\ \frac{5 x - 20 - 3 x + 15}{x - 5} & \leq 0 \\ \frac{2 x - 5}{x - 5} & \leq 0 \end{aligned}

Langkah kedua, kita tentukan titik kritis, yaitu pembuat nol pada pembilang dan penyebut.

Pembuat nol pada pembilang adalah

2 x - 5 = 0 \Leftrightarrow x = \frac{5}{2}

Pembuat nol pada penyebut adalah

x - 5 = 0 \Leftrightarrow x = 5

Langkah ketiga, kita buat garis bilangan kritis yang memuat beberapa daerah yang dibatasi oleh titik yang kita peroleh dari langkah kedua, dan perlu diingat pada titik kritis yang diperoleh dari penyebut digambarkan dengan tanda bulat meskipun tidak samaan yang sedang kita selesaikan

\leq

Langkah keempat , tentukan tanda masing-masing daerah pada garis bilangan dengan melakukan pengujian.

Pada garis bilangan di atas, kita memperoleh tiga daerah, yaitu

x \leq \frac{5}{2}

kita sebut saja "daerah kiri", daerah

\frac{5}{2} \leq x < 5

kita sebut sebagai "daerah tengah" dan daerah

x > 5

kita sebut sebagai "daerah kanan".

Pada masing-masing daerah tersebut kita ambil sembarang angka penguji, misal untuk daerah kiri

(x \leq \frac{5}{2})

saya ambil

x = 0

, untuk daerah tengah

(\frac{5}{2} \leq x < 5)

saya ambil

x = 3

, dan untuk daerah kanan

(x > 5)

saya ambil

x = 6

sebagai penguji. Dengan mensubstitusi titik-titik penguji tersebut ke fungsi rasional

\frac{2 x - 5}{x - 5}

maka kita memperoleh:

Titik Uji	$2 x - 5$	$x - 5$	$\frac{2 x - 5}{x - 5}$
$x = 0$	$(-)$	$(-)$	$\frac{(-)}{(-)} = (+)$
$x = 3$	$(+)$	$(-)$	$\frac{(+)}{(-)} = (-)$
$x = 6$	$(+)$	$(+)$	$\frac{(+)}{(+)} = (+)$ $\frac{(+)}{(+)} = (+)$

Langkah kelima , kita tentukan tentukan keseimbangan dengan kembali memperhatikan tanda-tanda pertidaksamaan dan tanda pada garis bilangan. Pertidaksamaan

\frac{2 x - 5}{x - 5} \leq 0

memiliki tanda pertidaksamaan

\leq

, dengan demikian penyelesaiannya adalah yang bertanda negatif atau nol

(\leq 0)

, yaitu daerah tengah pada garis bilangan tadi.

maka himpunan penyelesaian dari pertidaksamaan $\frac{5 x - 20}{x - 5} \leq 3$ adalah ${x | \frac{5}{2} \leq x < 5, x \in R}$ { x |

52≤ x < 5 , x ∈ R }

5. Nilai x yang memenuhi 2x+3/3x-7>0

a. 7/3>x> -3/2

b. x < -3/2 atau x > 7/3

c. -7/3 < x < 3/2

Jawab:

2x+3

x=-3/2

3x-7=0

x=7/3

6. Selesaikanlah Persamaan irasional,

[solusi]
tentukan terlebih dahulu prasyarat, yaitu:

Selanjutnya selesai :

Secara grafis persamaan diatas dapat di gambarkan sebagai berikut:

http://soulmath4u.blogspot.com/2013/10/persamaan-irasional.html

Dari grafik diatas, tampak bahwa berpotongan di titik A dan titik B. Maka himpunan kedua grafik adalah titik A, yaitu x = 2 (bagian yang bergaris tebal). Dan titik B, yaitu x = -2 adalah penyelesaian semu (bagian yang bergaris putus-putus).

7. Selesaikanlah Persamaan irasional berikut ini,

[Solusi]

Tentukan terlebih dahulu Prasyarat :

Selanjutnya selesai :

Penyelesaian dengan grafik, yaitu sebagai berikut:

8.Tentukan himpunan dari persamaan irasional berikut ini

, [Solusi]Tentukan terlebih dahulu prasyarat :

Selanjutnya diselesaikan:

Jadi, persamaan rasional,

tidak memiliki solusi

9. Syarat agar fungsi yang ada pada pertidaksamaan tersebut terdefinisi adalah x – 1 ≥ 0 dan 2 – x ≥ 0

x – 1 ≥ 0 2 – x ≥ 0

x ≥ 1 2 ≥ x

jadi 1 ≤ x ≤ 2

10. Nilai x yang memenuhi pertidaksamaan √x – 1 < √ 2 – x adalah

√x – 1 < √ 2 – x

x – 1 < 2 – x

2 x < 3

x < 3/2

Daftar Pustaka
Edumatika.Admin.2020,"Persamaan Dan Pertidakasamaan Rasioanal"https://edumatik.net/persamaan-dan-pertidaksamaan-rasional/.diakses pada tanggal 14 Desember 2021

m4th-lab.2018"Cara Menyelesaikan Pertidaksamaan Rasional atau Pertidaksamaan Pecahan Matematika Wajib kelas X"https://www.m4th-lab.net/2018/09/cara-menyelesaikan-pertidaksamaan.html#:~:text=Pertidaksamaan%20rasional%20adalah%20pertidaksamaan%20yang,ini%20beberapa%20contoh%20pertidaksamaan%20rasional.&text=Dengan%20f(x)%20sebagai%20fungsi,g(x)%E2%89%A00..diakses pada tangga 14 Desember 2021

Ruly.2013."Persamaan Irasional".https://soulmath4u.blogspot.com/2013/10/persamaan-irasional.html.diakses pada tanggal 14 Desember 2021

Kelas.Pintar.2021"Apa Itu Pertidaksamaan Irasional?"https://www.kelaspintar.id/blog/tips-pintar/apa-itu-pertidaksamaan-irasional-9251/.diakses pada tanggal 14 Desember 2021

Karmila

Selasa, 14 Desember 2021

Soal Komposisi Fungsi dan Fungsi Invers

Soal Persamaan Dan Pertidaksamaan Rasional Dan Irasional

Postingan Populer