Soal dan Pembahasan Fungsi Trigonometri

1. Tentukan nilai maksimum dan nilai minimum dari fungsi trigonometri di bawah in!

a. f(x) = 2 sin 2x + 5

b. f(x) = -3 cos 3(x+90°) - 8

Jawab:

a. f(x) = 2 sin 2x + 5 → a = 2 , c = 5

Nilai maksimum = |a| + c = |2| + 5 = 7

Nilai minimum = -|a| + c = -|2| + 5 = 3

b. f(x) = -3 cos 3(x+90°) - 8 → a = -3 , c = -8

Nilai maksimum = |a| + c = |-3| + |-8| = 11

Nilai minimum = -|a| + c = -|-3| + |-8| = 5

2. Perhatikan grafik fungsi berikut.

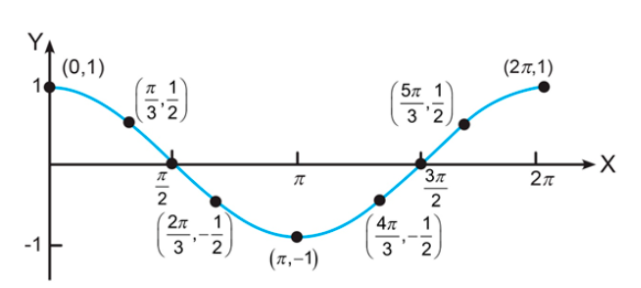
Grafik fungsi tersebut merupakan grafik fungsi jenis apa?

Pembahasan:

Jika diperhatikan, grafik tersebut dimulai dari titik (0,1) dan mempunyai periode satu putaran 0 ≤ x ≤ 2π.

Dengan demikian, grafik fungsi tersebut adalah grafik fungsi cos, yaitu y = cos x. Untuk meyakinkan, coba lihat salah satu titiknya.

Jadi, grafik fungsi tersebut merupakan grafik fungsi y = cos x untuk 0 ≤ x ≤ 2π.

3. Lukislah grafik fungsi y = 2 cos 2x, x ∈ [0^o, 360^o]

Pembahasan:

Untuk menentukan bentuk grafiknya, gunakan tabel trigonometri sudut istimewa.

Dengan demikian, grafik fungsi y = 2 cos 2x, x ∈ [0^o, 360^o] adalah sebagai berikut.

4. Hitunglah nilai maksimum dan minimum fungsi y = cos (x – 30), x ∈ [0^o, 360^o]. Kemudian, lukislah grafik fungsinya.

Pembahasan:

Berdasarkan tabel trigonometri untuk sudut istimewa, diperoleh:

Berdasarkan tabel di atas, nilai maksimum dari fungsi y = cos (x – 30), x ∈ [0^o, 360^o] adalah 1 dan nilai minimumnya adalah –1. Untuk lebih jelasnya, simak grafik fungsi berikut.

5. Tentukan nilai fungsi trigonometri berikut.

a. sin 105°

b. cos 15°

c. sin270° + cos270°

 Pembahasan:

a. sin 105° = sin (60° + 45°)

sin (60° + 45°) = sin 60° cos 45° + cos 60° sin 45°

= ½ √3 . ½ √2 + ½ . ½ √2

=  ¼ √6 + ¼ √2 = ¼ (√6 + √2)

b. cos 15° = cos (45° – 30°)

cos (45° – 30°) = cos 45° cos 30° + sin 45° sin30°

= ½ √2 . ½ √3 + ½ √2 . ½

= ¼  √6 + ¼ √2 = ¼ (√6 + √2)

c. sin270° + cos270°

Karena sin2x + cos2x = 1, maka sin270° + cos270° = 1

6. Gambar;ah grafik fungsi trigonometri f(x)=2 sin 2(x-45°)?

Pembahasan: 

a. Gambar garfik baku fungsi f(x)= sin x

b. Gambar grafik fungsi f(x)= 2sin x dengan ampliyudo a=2

c. Gambar grafik fungsi f(x)= 2 sin x dengan periode p=2π/k = 2π/2= 2

d. Gambar grafik fungsi f(x)= s sin 2(x-45°) dengan b=45° artinya grafik f(x)= 2sin2x digeser ke lanan karen abentuknya negatif sejauh 45°

Daftar Pustaka

Karina Dwi Adistiana.2018."Matematika Kelas 10 | Memahami Fungsi Trigonometri Sederhana"https://www.ruangguru.com/blog/memahami-fungsi-trigonometri-sederhana. diakses pada tanggal 16 Februari 2022

sereliciouz.2020."Grafik Fungsi Trigonometri – Matematika Kelas 10"https://www.quipper.com/id/blog/mapel/matematika/grafik-fungsi-trigonometri-matematika-kelas-10/. diakses pada tanggal 16 Februari 2022

Agustian.2022."Identitas Trigonometri: Persamaan, Grafik fungsi, Tabel, Sudut Istimewa, Contoh Soal"https://rumuspintar.com/identitas-trigonometri/. diakses pada tanggal 16 Februari 2022

Blog.Koma.2015."Grafik Fungsi Trigonometri"https://www.konsep-matematika.com/2015/11/grafik-fungsi-trigonometri.html. diakses pada tanggal 16 Februari 2022