Luas Segitiga Dengan Aturan Trigonometri, Aturan Sinus dan Aturan Cosinus

Luas Segitiga Dengan Aturan Trigonometri

Sebagaimana telah kita pelajari bahwa luas suatu segitiga dapat diperoleh dengan mengalikan alas dan tinggi dari segitiga tersebut dan kemudian membaginya dengan 2, atau dapat dituliskan sebagai

Selain menggunakan rumus di atas, luas segitiga tersebut juga dapat diperoleh dengan menggunakan rumus aturan trigonometri. Untuk penjelasannya, amatilah segitiga ABC berikut!

Perhatikan bahwa segitiga ABC pada Gambar 1 terbagi lagi menjadi dua segitiga yakni $\Delta ADC$ dan $\Delta BDC$. Pada $\Delta ADC$, kita peroleh

Dengan demikian,

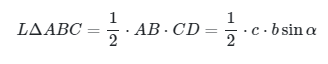
Jadi, luas $L\Delta ABC$ dapat dinyatakan sebagai

Dengan cara yang sama, untuk setiap segitiga ABC juga berlaku:

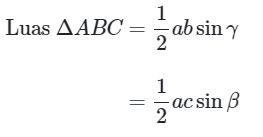
Luas Segitiga Jika Hanya Diketahui Panjang Ketiga Sisinya

Dari Gambar 1, jika diketahui hanya nilai ketiga sisinya maka luas segitiga ABC dapat juga ditentukan dengan rumus berikut.

di mana: $S=\frac{1}{2}(a+b+c)$.

Bukti:

Menurut identitas trigonometri diketahui bahwa

Jika persamaan (2) disubstitusikan ke (1) maka diperoleh:

di mana: $S=\frac{1}{2}(a+b+c)$

$<br>$

Contoh Soal:

1. Tentukan luas segitiga ABC pada Gambar 1 di atas jika diketahui sisi 

$BC=4$ cm, $AC=7\sqrt{3}$ cm dan $\angle C={60}^0$.

Pembahasan:

Diketahui $BC=a=4$ cm; $AC=b=7\sqrt{3}$ dan $\angle C={60}^0$. Dengan demikian, kita peroleh

2. Sebuah segitiga ABC diketahui luasnya 18 cm2. Jika panjang sisi 

$BC=4$ cm dan $AB=6\sqrt{3}$ cm, maka tentukanlah besar sudut B.

Pembahasan:

Diketahui luas segitiga = 18, $BC=a=4$; dan $AB=c=6\sqrt{3}$. Dengan demikian, kita peroleh

3. Hitunglah luas segitiga ABC jika diketahui panjang sisi-sisinya a = 16 cm, b = 14 cm, dan c = 10 cm!

Pembahasan:

Pertama, kita hitung

Sehingga luas segitiga ABC adalah

Jadi, luas segitiga ABC adalah $40\sqrt{3}$ cm2.

Aturan Sinus 

Menjelaskan hubungan antara perbandingan panjang sisi yang berhadapan dengan sudut terhadap sinus sudut pada segitiga. Berdasarkan aturan sinus dalam segitiga ABC, perbandingan panjang sisi dengan sinus sudut yang berhadapan dengan sisi segitiga mempunyai nilai yang sama. Seperti yang dijelaskan pada gambar di bawah ini.

Segitiga sembarang Δ ABC

Keterangan:

a = panjang sisi a

A = besar sudut di hadapan sisi a

b = panjang sisi b

B = besar sudut di hadapan sisi b

c = panjang sisi c

C = besar sudut di hadapan sisi c

Contoh Soal:

1. Sebuah segitiga diketahui memiliki sudut A = 30º, sisi a = 3 dan sisi b = 4. Hitung besar sudut B, besar sudut C dan panjang sisi c!

Diketahui:

A = 30º

a = 3

b = 4

Ditanya: B, C dan c?

Jawab:

• Menentukan besar sudut B

Karena sinus harus bernilai positif baik di kuadran I maupun kuadran II, maka sudut lain yang memenuhi adalah B = (180º - 41,8º) = 138,2º

• Menentukan besar sudut C

Jumlah sudut-sudut dalam segitiga adalah 180º, oleh karena itu berlaku:

A + B + C = 180º → C = 180º - (A + B)

Untuk B = 41,8º → C = 180º - (30º + 41,8º) = 108,2º

Untuk B = 138,2º → C = 180º - (30º + 138,2º) = 11,8º

• Menentukan panjang sisi C

Aturan Cosinus

Aturan Cosinus merupakan aturan yang menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga. Aturan cosinus dapat digunakan untuk menentukan unsur-unsur lain dalam suatu segitiga sembarang untuk dua kasus yaitu saat tiga sisi ketahui dan saat dua sisi dan sudut apitnya diketahui. Seperti yang dijelaskan pada gambar di bawah ini.

Segitiga sembarang Δ ABC

Keterangan:

a = panjang sisi a

A = besar sudut di hadapan sisi a

b = panjang sisi b

B = besar sudut di hadapan sisi b

c = panjang sisi c

C = besar sudut di hadapan sisi c

 

Sehingga aturan cosinus berlaku untuk setiap segitiga ABC sebagai berikut:

a² = b² + c² - 2 bc cos A

b² = c² + a² - 2 ac cos B

c² = a² + b² - 2 ab cos C

 

Berdasarkan rumus aturan cosinus di atas, maka di dapatkan rumus untuk menghitung besar sudutnya :

Contoh Soal:

1. Segitiga ABC diketahui panjang sisi a = 5 cm, panjang sisi c = 6 cm dan besar sudut B = 60º. Tentukan panjang sisi b!

Diketahui:

a = 5 cm

c = 6 cm

B = 60º

Ditanya: b?

Jawab:

 b² = a² + c² - 2ac cos B

 b² = 5² + 6² - 2(5)(6) cos 60º

 b² = 25 + 36 - 60 (0,5)

 b² = 61 - 30

 b² = 31

 b = 5,56 cm

Jadi, panjang sisi b adalah 5,56 cm

Daftar Pustaka

Ji Long.Tju.2014"Luas Segitiga dengan Aturan Trigonometri"https://jagostat.com/matematika-dasar/luas-segitiga-dengan-aturan-trigonometri.diakses pada tanggal 24 Januari tahun 2022

Suwarno.Muji.2017."Luas Segitiga Dalam Trigonometri"https://www.materimatematika.com/2017/10/luas-segitiga-dalam-trigonometri.html.diakses pada tanggal 24 Januari tahun 2022

Dwi Adistina .Karina.2018."Matematika Kelas 10 | Apa Itu Aturan Sinus dan Cosinus?"https://www.ruangguru.com/blog/apa-itu-aturan-sinus-dan-cosinus.diakses pada tanggal 24 Januari tahun  2022

Koordinat Kutub dan Koordinat Kartesius

 

Hubungan Koordinat Kartesius dengan Koordinat Polar (Kutub)

Hubungan antara koordinat kartesius dan koordinat polar ditunjukan dengan jarak titik asal O (0,0) dengan titik P (x, y). Jarak tersebut dapat dinamakan dengan jarak r. Untuk memperoleh nilai r tersebut dapat menggunakan rumus di bawah ini:

Kemudian koordinat kartesius dan koordinat polar akan menghasilkan sebuah sudut α. Sudut α ialah sudut yang terletak diantara garis hubung P terhadap titik O (0,0) dengan sumbu X positif. Namun perhitungannya berlawanan arah dengan arah pada jarum jam. Titik P tersebut dapat dinyatakan dalam bentuk koordinat kutub yaitu P (r, α).

Koordinat kartesius dengan koordinat polar dapat digambar menjadi grafik seperti di bawah ini:

Titik pusat pada koordinat kutub memiliki letak titik P yang dapat digambarkan dengan (r, α). r menunjukan jarak OP, sedangkan α menunjukan sudut antara sumbu OX positif dengan OP. Untuk itu perhitungan besar sudut α berawal dari sumbu OX positif dan berputar berkebalikan dengan arah jarum jam.

Persamaan dan Perbedaan Koordinat Kartesius Dengan Koordinat Polar

Persamaan antara kartesius dengan polar ialah sama sama termasuk koordinat Matematika. Namun jika ditinjau dari segi perbedaannya, maka dapat anda perhatikan penjelasan masing masing koordinat yaitu meliputi:

Koordinat Kartesius

Peletakkan titik P pada kartesius dapat ditunjukan dalam bentuk himpunan pasangan berurutan yakni P (x, y), dimana :

• Koordinat x disebut absis, yakni jarak antara titik menuju sumbu Y.
• Koordinat y disebut ordinat, yakni jarak antara titik menuju sumbu X.

Koordinat Polar (Kutub)

Letak P pada koordinat kutub dapat digambarkan dalam bentuk ukuran jarak r dengan sudut α. Dimana:

• Jarak r ialah jarak anatara titik P (x, y) menuju titik asal O (0,0). Untuk memperoleh besar jarak r dapat menggunakan rumus pythagoras yakni r² = x² + y².
• Titik P pada koordinat kutub dapat digambarkan dalam bentuk P (r, α).
• Sudut α ialah sudut yang dibentuk antara garis hubung pada titik P terkadap titik O (0,0) dengan sumbu X positif, dimana peritungan arahnya berkebalikan dengan arah jarum jam.

Mengubah Koordinat Kartesius Menjadi Koordinat Polar

Dalam mengubah koordinat kartesius menjadi koordinat polar dapat dilakukan dengan membuat sebuah grafik yang menghubungkan kedua koordinat Matematika tersebut. Jika keduanya digabungkan dalam satu koordinat, maka akan membentuk sebuah segitiga siku siku dimana panjang sisinya berupa sisi x, y dan r. Untuk memperoleh jarak r dapat menggunakan konsep teorema pythagoras yakni:

Selain menerapkan konsep teorema pythagoras, tetapi juga menerapkan perbandingan trigonometri seperti di bawah ini:

Kesimpulan:
Untuk mengubah koordinat kartesius (x, y) menjadi koordinat polar (r, α), maka menggunakan aturan seperti di bawah ini:

Mengubah Koordinat Polar Menjadi Koordinat Kartesius

Dalam mengubah koordinat polar menjadi koordinat kartesius dapat dilakukan dengan membuat sebuah grafik yang menghubungkan kedua koordinat Matematika tersebut. Jika keduanya digabungkan dalam satu koordinat, maka akan membentuk sebuah segitiga siku siku dimana panjang sisinya berupa sisi x, y dan r.  Dalam mengubah koordinat kutub menjadi kartesius pada dasarnya menggunakan konsep perbandingan trigonometri seperti di bawah ini:

Kesimpulan:
Untuk mengubah koordinat polar (r, α) menjadi koordinat kartesius (x, y), maka menggunakan aturan seperti di bawah ini:

Contoh Soal:

1. Nyatakan titik-titik berikut ini kedalam koordinat kutub atau koordinat kartesius (sesuai dengan yang diketahui). 

a. P(4,4) 

b. P(6,120° ) 

Penyelesaian: a. P(4,4)

 

Jadi koordinat kutubnya adalah P(4√2,45°)

b. P(6,120°)

Jadi koordinat titik P(-3.3√3)

Daftar Pustaka

Kahfi.bilal.2021."Mengenal Koordinat Kartesius dan Polar dalam Matematika"http://www.antotunggal.com/2021/10/mengenal-koordinat-kartesius-dan-polar.html#.diakses pada tanggal 17 Januari 2022

Sumberbelajar."Mengkonversi Koordinat Cartesius ke Koordinat Kutub (Polar)"https://sumberbelajar.seamolec.org/Media/Dokumen/59c1c6b6865eacac04e3cd2a/c2f20d6ff4bc0d4a3bcd7a20a291ad09.pdf.diakses pada tanggal 17 Januari 2022