Persamaan dan Pertidaksamaan Irasional

 Persamaan Irasional

Persamaan  irasional ( irrational equation ) adalah persamaan yang melibatkan variabel dalam tanda akar. Lima contoh berikut semuanya merupakan persamaan irasional

Bentuk Umum Persamaan irasional 

Secara umum  berbentuk seperti dibawah ini:

 f(x) dan g(x)  merupakan suatu polinomial (suku banyak).

Contoh Soal:

1. Selesaikanlah Persamaan irasional,

  

[solusi]
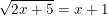
tentukan terlebih dahulu prasyarat, yaitu:

Selanjutnya selesai :

Secara grafis persamaan diatas dapat di gambarkan sebagai berikut:

Dari grafik diatas, tampak bahwa berpotongan di titik A dan titik B. Maka himpunan kedua grafik adalah titik A, yaitu x = 2 (bagian yang   bergaris tebal). Dan titik B, yaitu x = -2 adalah penyelesaian semu (bagian yang bergaris putus-putus).

2. Selesaikanlah Persamaan irasional berikut  ini,

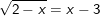[Solusi]

Tentukan terlebih dahulu Prasyarat :
  

Selanjutnya selesai :

  

Penyelesaian dengan grafik, yaitu sebagai berikut:

3.

Tentukan himpunan dari   persamaan irasional berikut  ini , [Solusi]Tentukan terlebih dahulu prasyarat :
Selanjutnya diselesaikan:
Jadi, persamaan rasional, 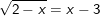  tidak memiliki solusi. 

Pertidaksaam Irasioanl

Pertidaksamaan irasional atau pertidaksamaan bentuk akar adalah pertidaksamaan yang memuat fungsi irasional atau bentuk akar. Pertidaksamaan irasional yang akan dipelajari kali ini adalah pertidaksamaan irasional satu variabel, dimana ada beberapa bentuk umum yang diketahui dari ini, diantaranya :

1. √f(x) < a √f(x) < √g(x)
2. √f(x) ≤ a √f(x) ≤  √g(x)
3. √f(x) > a √f(x)> √g(x)
4. √f(x) ≥ a √f(x) ≥ √g(x)

f (x) dan g (x) adalah fungsi polynomial, f (x), g (x) ≥ 0, a adalah konstanta.

Dalam menentukan himpunan penyelesaian pertidaksamaan irasional yang diubah menjadi pertidaksamaan satu variable ada beberapa sifat yang perlu dipahami antara lain :

jika √f(x) < a dengan f (x) ≥ 0, dan a ≥ 0, maka f (x) <a2

jika √f(x) ≤ a dengan f (x) ≥ 0, dan a ≥ 0, maka f (x) ≤ a2

jika √f(x) > a dengan f (x) ≥ 0, maka f (x) > a2

jika √f(x) ≥ a dengan f (x) ≥ 0, maka f (x) ≥ a2

jika √f(x) < √g(x) dengan f (x), g (x) ≥ 0, maka f (x) < g (x)

jika √f(x) ≤ √g(x) dengan f (x), g (x) ≥ 0, maka f (x) ≤ g (x)

jika √f(x) > √g(x) dengan f (x), g (x) ≥ 0, maka f (x) > g (x)

jika √f(x) ≥ √g(x) dengan f (x), g (x) ≥ 0 maka f (x) ≥ g (x)

Metode Penyelesaian Pertidaksamaan Irasional

Himpunan penyelesaian pertidaksamaan irasional dapat ditentukan dengan langkah-langkah berikut ini :

• Tentukan syarat batas nilai x agar fungsi yang ada di dalam akar terdefinisi.
• Kuadratkan kedua ruas pertidaksamaan sehingga bentuk akar menghilang.
• Tentukan himpunan penyelesaian dari pertidaksamaan yang diperoleh pada langkah 2.
• Gambarkan daerah himpunan penyelesaian yang diperoleh pada langkah 3 dan syarat batas nilai x yang diperoleh pada langkah 1 dalam suatu garis bilangan.
• Tentukan daerah himpunan penyelesaian pertidaksamaan pada langkah 4. daerah himpunan penyelesaian pertidaksamaan irasional adalah daerah yang memuat nilai x yang memenuhi langkah 3 dan 1.

Adapun contoh soalnya adalah : Tentukan himpunan penyelesaian pertidaksamaan irasional

√x – 1 < √2 – x

penyelesaian :

1. Syarat agar fungsi yang ada pada pertidaksamaan tersebut terdefinisi adalah x – 1 ≥ 0 dan 2 – x ≥ 0

x – 1 ≥ 0             2 – x ≥ 0

x ≥ 1                  2 ≥ x

jadi 1 ≤ x ≤ 2

2. Nilai x yang memenuhi pertidaksamaan adalah

√x – 1 < √ 2 –  x

x – 1 < 2 – x

2 x < 3

x < 3/2

Daftar Pustaka

Ruly.2013."Persamaan Irasional".https://soulmath4u.blogspot.com/2013/10/persamaan-irasional.html.diakses pada tanggal 14 Desember 2021

Kleas.Pintar.2021"Apa Itu Pertidaksamaan Irasional?"https://www.kelaspintar.id/blog/tips-pintar/apa-itu-pertidaksamaan-irasional-9251/.diakses pada tanggal 14 Desember 2021