Karmila: Oktober 2021

Sistem Pertidaksamaan Kuadrat Linear

Pertidaksamaan linear dua variabel memuat dua variabel berpangkat satu yang memuat tanda ketidaksamaan

Pertidaksamaan kuadrat dua variabel adalah pertidaksamaan yang memuat dua variabel dengan derajat tertinggi dua. Penyelesaian pertidaksamaan kuadrat dua pada dasarnya sama dengan penyelesaian pertidaksamaan linear dua variabel.

Contoh Soal Pertidaksamaan Linear

1. 3x + 2y < 8

x + y < 3

Tentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel tersebut jika x dan y merupakan bilangan bulat positif

Jawab:

Dengan menggunakan grafik, dibuat garis 3x + 2y = 8, kemudian tentukan bagian yang merupakan 3x + 2y < 8.

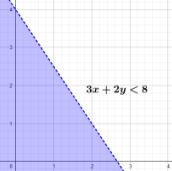
Sistem Pertidaksamaan Linear Dua Variabel

Dengan menggunakan grafik, dibuat garis x + y = 3, kemudian tentukan bagian yang merupakan x + y < 3.

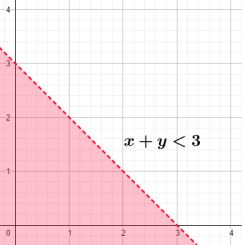
Contoh Sistem Pertidaksamaan Linear Dua Variabel

Kemudian tentukan titik potong kedua garis tersebut.

3x + 2y = 8

x + y = 3

Dengan menggunakan metode eliminasi diperoleh:

3x + 2y = 8

2x + 2y = 6

————– –

x = 2

Substitusikan nilai x = 2 ke persamaan x + y = 3

2 + y = 3

y = 3 – 2

y = 1

Titik potong kedua garis tersebut adalah (2, 1).

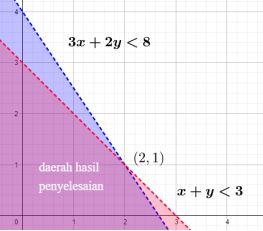
Daerah berwarna ungu merupakan daerah hasil penyelesaian sistem pertidaksamaan linear dua variabel.

2. Tentukan solusi pertidaksamaan linear berikut ini untuk nilai variabel merupakan bilangan bulat positif.

3x < 12
2y > 6

Pembahasan

1. 3x < 12

x < 12/3

x < 4

Solusi: {1, 2, 3}

2. 2y > 6

y > 6/2

y > 3

Solusi : {4, 5, 6, . . .}

Contoh Soal Pertidaksamaan Kuadrat

1. Tentukan HP dari −x² − 3x + 4 > 0

Jawab
Pembuat nol
−x² − 3x + 4 = 0
x² + 3x − 4 = 0
(x+4) (x−1) = 0
x = −4 atau x = 1

Untuk interval −4 < x < 1, ambil x = 0
−x² − 3x + 4 = −(0)² − 3(0) + 4 = 4 (+)

Karena pertidaksamaan bertanda “>” , Jadi, daerah penyelesaian ada pada interval yang bertanda (+).
∴ HP = {−4 < x < 1}

2. Himpunan penyelesaian dari pertidaksamaan kuadrat x2 – 5x – 6 > 0 untuk x ∈ R adalah …

A. {x|x < -1 atau x > 6}
B. {x|x < 2 atau x > 3}
C. {x|-3 < x < 2}
D. {x|x < -6 atau x > 6}
E. {x|-6 < x < 1}

Pembahasan / penyelesaian soal

Cara menjawab soal ini sebagai berikut:

→ x2 – 5x – 6 > 0
→ (x – 6)(x + 1) > 0
→ x1 = 6 atau x2 = -1

Untuk menentukan tanda garis bilangan kita subtitusikan angka yang lebih kecil dari -1 (misalkan x = – 2) ke pertidaksamaan kuadrat x2 – 5x – 6 = (-2)2 – 5 (-2) – 6 = 4 + 10 – 6 = + 9

Hasilnya positif sehingga tanda garis bilangan diawali positif (+ , – , +):

Karena notasi pertidaksamaan lebih dari (>) maka himpunan penyelesaian ditunjukkan oleh garis bilangan dengan tanda positif atau pada interval {x|x < -1 atau x > 6}. Jadi soal ini jawabannya A.

Contoh Soal Pertidaksamaan Kuadrat Linear

1. 1. Sketsalah grafik dari sistem pertidaksamaan kuadrat-linear dari

$\left\{\begin{matrix} y & \geq & x^{2} \\ y & < & x & +&2 \end{matrix}\right.$

Jawab:

Untuk menyelesaikan sketsa grafik dari pertidaksamaan soal tersebut di atas, coba perhatikanlah langkah berikut;

untuk $y\geq x^{2}$ ,

$\begin{tabular}{|r|r|c|c|c|c|}\hline x&-2&-1&0&1&2\\\hline y&4&1&0&1&4\\\hline (x,y)&(-2,4)&(-1,1)&(0,0)&(1,1)&(2,4)\\\hline \end{tabular}$

untuk $y< x+2$

$\begin{tabular}{|r|r|c|c|c|c|}\hline x&-2&-1&0&1&2\\\hline y&0&1&2&3&4\\\hline (x,y)&(-2,0)&(-1,1)&(0,2)&(1,3)&(2,4)\\\hline \end{tabular}$

Langkah berikutnya gunakan titik uji untuk mengetahui daerah penyelesaian yang dimaksud, misalkan kita ambil contoh $titik\: (1,1)$ , kemudian kita cobakan ke kedua pertidaksamaan tersebut.

Langkah berikutnya membuat sketsa grafik yang diinginkan dari

$\left\{\begin{matrix} y & \geq & x^{2} \\ y & < & x & +&2 \end{matrix}\right.$

perhatikanlah hasil akhir berikut

2. Sketsalah grafik dari sistem pertidaksamaan berikut

$\left\{\begin{matrix} x^{2}&+&y^{2}&\geq &4 \\ x^{2}&+&y^{2}&< &9 \end{matrix}\right.$

Jawab:

Untuk menyelesaikan sketsa grafik dari pertidaksamaan soal tersebut di atas, coba perhatikanlah pula langkah berikut;

kedua pertidaksamaan di atas adalah (persamaan) lingkaran

lingkaran yang berada di dalam adalah $x^{2}+y^{2}=4$ adalah sebuah persamaan lingkaran dengan pusat di (0,0) dan berjari-jari 2. Sedangkan lingkaran yang berada di sisi luar (yang besar) memiliki persamaan $x^{2}+y^{2}=9$ adalah persamaan lingkaran yang berpusat di (0,0) dan berjari-jari 3.

Perhatikanlah tabel berikut

$\begin{array}{|c|c|c|c|c|}\hline No&Lingkaran1&lingkaran2&Pusat&jari-jari\\\hline 1&x^{2}+y^{2}=4&&(0,0)&2\\\hline 2&&x^{2}+y^{2}=9&(0,0)&3\\\hline \end{array}$

Sebagai perbandingan hasil pengecekannya,

$\begin{array}{|c|c|c|c|}\hline \multicolumn{4}{|c|}{Lingkaran1;\quad x^{2}+y^{2}\geq 4}\\\hline No&Titik\quad uji&Proses&Hasil/Keterangan\\\hline 1&(0,0)&0^{2}+0^{2}\geq 4&Salah\\\hline 2&(1,1)&1^{2}+1^{2}\geq 4&Salah\\\hline 3&(2,2)&2^{2}+2^{2}\geq 4&Benar\\\hline 4&(3,3)&3^{2}+3^{2}\geq 4&Benar\\\hline 5&(4,4)&4^{2}+4^{2}\geq 4&Benar\\\hline \cdots &\cdots &\cdots &\cdots \\\hline \vdots &dst&dst&dst\\\hline \end{array}\qquad \begin{array}{|c|c|c|c|}\hline \multicolumn{4}{|c|}{Lingkaran2;\quad x^{2}+y^{2}< 9}\\\hline No&Titik\quad uji&Proses&Hasil/Keterangan\\\hline 1&(0,0)&0^{2}+0^{2}< 9&Benar\\\hline 2&(1,1)&1^{2}+1^{2}< 9&Benar\\\hline 3&(2,2)&2^{2}+2^{2}< 9&Benar\\\hline 4&(3,3)&3^{2}+3^{2}< 9&Salah\\\hline 5&(4,4)&4^{2}+4^{2}< 9&Salah\\\hline \cdots &\cdots &\cdots &\cdots \\\hline \vdots &dst&dst&dst\\\hline \end{array}$ .

Sebagai langkah akhir tinggal kita sketsa saja grafik yang diinginkan yaitu

Daftar Pustaka

Rahmah.Azzahra.2020."Pertidaksamaan Kuadrat : Langkah Penyelesaian dan Contoh Soal" https://rumus.co.id/pertidaksamaan-kuadrat/. diakses pada 1 Oktober 2021

Agustian.2021."Pertidaksamaan Linear: Pengertian, Sistem Soal". https://rumuspintar.com/pertidaksamaan-linear/. di akses pada tanggal 1 Oktober 2021

Ahmadthohir1089.2014."Sistem Pertidaksamaan Kuadrat Dua Variabel (SPtLDV)".https://ahmadthohir1089.wordpress.com/2014/10/20/moga-bisa-dilanjut/. diakses pada tanggal 1 Oktober 2021

Karmila

Jumat, 01 Oktober 2021

Sistem Pertidaksamaan Kuadrat Linear

Postingan Populer