Sistem Persamaan Linear Dua Variabel (SPLDV)

Sistem Persamaan Linear Dua Variabel (SPLDV)

Definisi dan Bentuk Umum

Sistem persamaan linear dua variabel (peubah) atau disingkat SPLDV adalah suatu persamaan matematika yang terdiri atas dua persamaan linear yang masing-masing bervariabel dua (misal x dan y).  Dengan demikian, bentuk umum dari Sistem Persamaan Linear Dua Variabel dalam x dan y dapat kita tuliskan sebagai berikut.

ax + by = c	atau	a1x + b1y = c1
px + qy = r		a2x + b2y = c2

Metode Penyelesaian SPLDV

1. Metode Grafik

Cara yang paling mudah untuk menggambar grafik adalah dengan mencari titik potong terhadap sumbu x dan sumbu y

Contoh:

1. Gambarkan grafik untuk persamaan 2x + y = 4.

Penyelesaian:

Untuk menggambarkan grafik SPLDV, gunakan paling sedikit dua titik seperti pada tabel berikut.

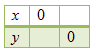
Tentukan nilai y untuk x = 0.
2x + y = 4
⇔2( 0) + y = 4
⇔y = 4

Tentukan nilai x untuk y = 0.
2x + y = 4
⇔ 2x + 0 = 4
⇔ 2x = 4
⇔ x = 2

Tuliskan hasil yang diperoleh ke dalam tabel.

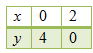
Ini berarti, titik yang diperoleh adalah A (0, 4) dan B (2, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

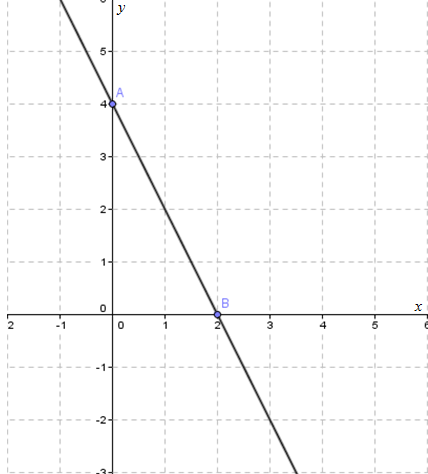
2. Tentukan penyeselesaian dari SPLDV:

2x + y = 6
2x + 4y = 12

Penyelesaian:

Langkah 1: gambarkan grafik untuk persamaan pertama.

Gunakan paling sedikit dua titik seperti pada tabel berikut.

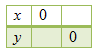
Tentukan nilai y untuk x = 0.
2x + y = 6
⇔ 2(0) + y = 6
⇔ y = 6

Tentukan nilai x untuk y = 0.
2x + y = 6
⇔2x + 0 = 6
⇔2x = 6
⇔x = 3

Tuliskan hasil yang diperoleh ke dalam tabel.

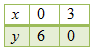
Ini berarti, titik yang diperoleh adalah A (0, 6) dan B (3, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

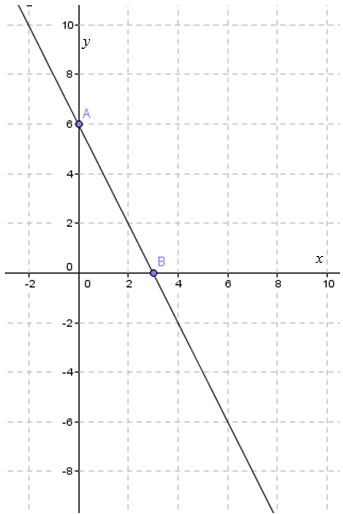
2. Metode Eliminasi

Metode ini bertujuan untuk mengeliminasi salah satu variabel untuk mengetahui nilai variabel lainnya.

Contoh:

1. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan 2x+y=7 dan x−y=8 dengan metode eliminasi!

Pembahasan:
2x+y=7 . . . . (1)
x−y=8 . . . . (2)

Eliminasi suku variabel x: samakan koefisien x dengan mengalikan persamaan (1) dengan 1 dan dengan mengalikan persamaan 2 dengan 2, kemudian kurangkan.
2x+y=7x−y=8  |×1×2 |

   2x+y=72x−2y=16   −_
3y=−9
y=−3

Eliminasi suku variabel y: koefisien y pada persamaan (1) dan (2) hanya berbeda tanda, tidak perlu disamakan. Cukup hanya dengan menjumlahkan kedua persamaan.

   2x+y=7x−y=8   +_
3x=15
x=5

HP={(5,−3)}

2. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan 

$3x-4y=5$ dan $2x+3y=-8$ dengan cara atau metode eliminasi!

Pembahasan:
$3x-4y=5$ . . . . (1)
$2x+3y=-8$ . . . . (2)

Eliminasi suku variabel $x$: kalikan persamaan (1) dengan 2 dan kalikan persamaan (2) dengan 3, kemudian kurangkan.

$\begin{array}{c}3x-4y=5\\ 2x+3y=-8\end{array}|\begin{array}{c}\times 2\\ \times 3\end{array}|$

$\underset{-}{{\begin{array}{c}6x-8y=10\\ 6x+9y=-24\end{array}}_{-}}$
$-17y=34$
$y=-2$

Eliminasi suku variabel $y$: kalikan persamaan (1) dengan 3 dan kalikan persamaan (2) dengan 4. Karena koefisien $y$ pada persamaan (1) dan (2) hanya berbeda tanda, lakukan penjumlahan.

$\begin{array}{c}3x-4y=5\\ 2x+3y=-8\end{array}|\begin{array}{c}\times 3\\ \times 4\end{array}|$

$\underset{-}{{\begin{array}{c}9x-12y=15\\ 8x+12y=-32\end{array}}_{+}}$
$17x=-17$
$x=-1$

$HP=\left\{\right(-1,-2\left)\right\}$

3. Metode Subtitusi

Metode substitusi bertujuan untuk mengganti nilai suatu variabel di suatu persamaan dari persamaan lainnya.

Contoh:

1. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan x=2 dan 3x+2y=12 dengan metode substitusi!

Pembahasan:
Nilai dari x sudah diketahui, tinggal memasukkan nilai x=2 ke dalam persamaan 3x+2y=12.
3x+2y=12
3.2+2y=12
6+2y=12
2y=12−6
2y=6
y=3

HP={(2,3)}

2. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan $y=x+5$ dan $3x-y=7$ dengan metode substitusi!

Pembahasan:
$y=x+5$ . . . . (*)
$3x-y=7$ . . . . (**)

Persamaan (*) sudah dalam bentuk eksplisit, dengan begitu bisa langsung disubstitusikan ke dalam persamaan (**).
$3x-y=7$
$3x-(x+5)=7$ → jangan lupa tanda kurung.
$3x-x-5=7$
$2x=7+5$
$2x=12$
$x=6$

Substitusikan nilai $x=6$ kedalam persamaan (*) atau persamaan (**) untuk mendapatkan nilai dari $y$. Dalam hal ini kita ambil persamaan (*).
$y=x+5$
$y=6+5$
$y=11$

$HP=\left\{\right(6,11\left)\right\}$

4. Metode Gabungan

Metode ini merupakan gabungan dari metode eliminasi dan substitusi. Caranya, kamu dapat menggunakan metode eliminasi untuk mencari nilai x terlebih dahulu, kemudian ganti variabel x dengan nilai x yang sudah diperoleh dengan menggunakan metode substitusi untuk memperoleh nilai y.

Contoh:

1. Diketahui persamaan  x + 3y = 15 dan 3x + 6y = 30, dengan menggunakan metode campuran tentukanlah Himpunan penyelesaiannya !

Penyelesaian :

Diketahui :

Persamaan 1 = x + 3y = 15

Persamaan 2 = 3x + 6y = 30

Langkah Pertama Menggunakan Metode Eliminasi :

x + 3y = 15  | x3| <=> 3x +9x = 45

3x + 6y = 30  | x1| <=> 3x + 6y = 30    _

                                            0 + 3y = 15

                                              y = 5

Langkah Kedua Menggunakan Metode Substusi :

x + 3y = 15
x + 3.5 = 15
x + 15 = 15
x = 0

Jadi himpunan penyelesaian dari soal diatas adalah HP ={ 0 , 5 }