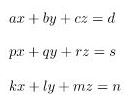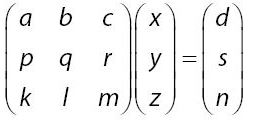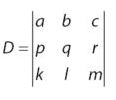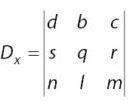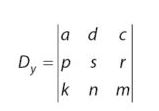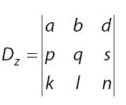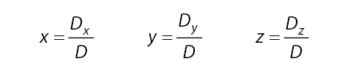Sistem Persamaan Linear Tiga Variabel (SPLTV)

Definisi

Sistem persamaan linear tiga variabel (SPLTV) adalah bentuk perluasan dari  persamaan linear dari dua variabel (SPLDV).

Bentuk yang umum dari Sistem Persamaan Linear Tiga Variabel (SPLTV) di dalam x, y, dan juga z bisa ditulis seperti berikut ini :

ax + by + cz = d                                  a1x + b1y + c1z = d1

ex + fy + gz = h             atau              a2x + b2y + c2z = d 2
ix + jy + kz = l                                     a3x + b3y + c3z = d3

Dengan demikian ⇒ a, b, c, d, e, f, g, h, i, j, k, dan l atau a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, dan d3 = merupakan bentuk  bilangan-bilangan real.

Keterangan :

• a, e, I, a1, a2, a3 = ialah bentuk koefisien dari x.
• b, f, j, b1, b2, b3 = ialah bentuk koefisien dari y.
• c, g, k, c1, c2, c3 = ialah bentuk koefisien dari z.
• d, h, i, d1, d2, d3 = ialah bentuk konstanta.
• x, y, z = ialah variabel atau peubah.

1. Metode Gabungan

Penyelesaian sistem persamaan linear dengan menggunakan metode gabungan/campuran merupakan cara penyelesaian dengan menggabungkan dua metode sekaligus, yakni metode eliminasi dan metode subtitusi. Metode ini bisa dikerjakan dengan subtitusi terlebih dahulu atau dengan eliminasi terlebih dahulu. 

Contoh:

1.Tentukan himpunan penyelesaian sistem persamaan linear tiga variabel di bawah ini dengan menggunakan metode gabungan.

x + 3y + 2z = 16

2x + 4y – 2z = 12

x + y + 4z = 20

Penyelesaian:

·         Metode substitusi

Pertama, kita tentukan dulu persamaan yang paling sederhana. Dari ketiga persamaan yang ada, persamaan ketiga lebih sederhana. Dari persamaan ketiga, nyatakan variabel z sebagai fungsi y dan z sebagai berikut.

⇒ x + y + 4z = 20

⇒ x = 20 – y – 4z ............... Pers. (1)

Kemudian, subtitusikan persamaan (1) di atas ke dalam SPLTV pertama.

⇒ x + 3y + 2z = 16

⇒ (20 – y – 4z) + 3y + 2z = 16

⇒ 2y – 2z + 20 = 16

⇒ 2y – 2z = 16 – 20

⇒ 2y – 2z = –4

⇒ y – z = –2 ............... Pers. (2)

 

Lalu, subtitusikan persamaan (1) di atas ke dalam SPLTV kedua.

⇒ 2x + 4y – 2z = 12

⇒ 2(20 – y – 4z) + 4y – 2z = 12

⇒ 40 – 2y – 8z + 4y – 2z = 12

⇒ 2y – 10z + 40 = 12

⇒ 2y – 10z = 12 – 40

⇒ 2y – 10z = –28  ............... Pers. (3)

Dari persamaan (2) dan persamaan (3) kita peroleh SPLDV y dan z berikut.

y – z = –2

2y – 10z = –28 

•   Metode eliminasi

Untuk mengeliminasi y, maka kita kalikan SPLDV pertama dengan 2 agar koefisien y kedua persamaan sama. Selanjutnya kita selisihkan kedua persamaan sehingga kita peroleh nilai z sebagai berikut.

y – z	=	–2	|× 2|	→	2y – 2z	=	–4
2y – 10z	=	–28	|× 1|	→	2y – 10z	=	–28	−
					8z	=	24
					Z	=	3

 

Untuk mengeliminasi z, maka kalikan SPLDV pertama dengan 10 agar koefisien z kedua persamaan sama. Selanjutnya kita kurangkan kedua persamaan sehingga diperoleh nilai y sebagai berikut.

y – z	=	–2	|× 10|	→	10y – 10z	=	–20
2y -10z	=	–28	|× 1|	→	2y – 10z	=	–28	−
					8y	=	8
					y	=	1

Sampai tahap ini, kita peroleh nilai y = 1 dan z = 3. Langkah terakhir yaitu menentukan nilai x. Cara menentukan nilai x adalah dengan memasukkan nilai y dan z tersebut ke dalam salah satu SPLTV, misalnya x + 3y + 2z = 16 sehingga kita peroleh:

⇒ x + 3y + 2z = 16

⇒ x + 3(1) + 2(3) = 16

⇒ x + 3 + 6 = 16

⇒ x + 9 = 16

⇒ x = 16 – 9

⇒ x = 7

 

Dengan demikian kita peroleh nilai x = 7, y = 1 dan z = 3 sehingga himpunan penyelesaian SPLTV di atas adalah {(7, 1, 3)}.

2. Metode Determinan Matriks

Apabila diketahui tiga persamaan linear dengan bentuk  tiga variabel (x, y, dan z) terlihat pada persamaan seperti di bawah ini.

Bentuk dari SPLTV seperti di atas dalam bentuk matriks bisa dibuat seperti berikut.

Berdasarkan bentuk matriks di atas, bisa disusun determinan yang utama, determinan bentuk variabel x, determinan dari variabel y, dan memiliki determinan variabel z. Untuk lebih jelas, maka perhatikan masing-masing bentuk determinan pada daftar yang tertera di bawah.

1. Determinan utama
   

2. Determinan variabel x
   

3. Determinan variabel y
   

4. Determinan variabel z
   

Selanjutnya jika ingin mengetahui nilai masing-masing dari variabel x, y, dan z bisa mengunakan rumus berikut ini.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan linier tiga variable

2x + y + z = 12

x + 2y – z = 3

3x – y +z = 11

Penyelesaian:

Pertama kita ubah bentuk sistem persamaan di atas kedalam bentuk matriks

 

Kemudian kita tentukan determinan matriks D, Dx, Dy, dan Dz. Matriks D adalah matriks 3 x 3 yang elemen-elemennya terdiri atas koefisien-koefisien semua variabel persamaan. Matriks Dx adalah matriks 3 x 3 yang elemen kolom pertamanya merupakan konstanta persamaan, kemudian kolom kedua terdiri atas koefisien y, dan kolom ketiga terdiri  atas koefisien z. Matriks Dy adalah matriks 3 x 3 yang elemen kolom pertamnya terdiri atas koefisien x, kolom kedua terdiri atas konstanta persamaan, dan kolom ketiga terdiri atas koefisien z. Sedangkan, matriks Dz adalah matriks 3 x 3 yang elemen kolom pertamanya terdiri atas koefisien x, kolom kedua terdiri atas koefisien y, dan kolom ketiga terdiri atas konstanta persamaan. Sehingga,

Daftar Pustaka

De.Bang.2020."Penyelesaian SPLTV Metode Campuran"https://subdigmatika.blogspot.com/2020/11/penyelesaian-spltv-dengan-metode_12.html diakses pada tnggal 27 Agustus 2021

Matematika.Blog.2017."Cara Menentukan Penyelesaian SPLTV Metode Gabungan atau Campuran"https://blogmipa-matematika.blogspot.com/2017/10/penyelesaian-SPLTV-metode-campuran.html.diakses pada tnggal 27 Agustus 2021

Rada.2021."Sistem Persamaan Linear Tiga Variabel (SPLTV)"https://dosenpintar.com/spltv/.diakses pada tanggal 27 Agustus 2021

Sistem Persamaan Linear Dua Variabel (SPLDV)

Sistem Persamaan Linear Dua Variabel (SPLDV)

Definisi dan Bentuk Umum

Sistem persamaan linear dua variabel (peubah) atau disingkat SPLDV adalah suatu persamaan matematika yang terdiri atas dua persamaan linear yang masing-masing bervariabel dua (misal x dan y).  Dengan demikian, bentuk umum dari Sistem Persamaan Linear Dua Variabel dalam x dan y dapat kita tuliskan sebagai berikut.

ax + by = c	atau	a1x + b1y = c1
px + qy = r		a2x + b2y = c2

Metode Penyelesaian SPLDV

1. Metode Grafik

Cara yang paling mudah untuk menggambar grafik adalah dengan mencari titik potong terhadap sumbu x dan sumbu y

Contoh:

1. Gambarkan grafik untuk persamaan 2x + y = 4.

Penyelesaian:

Untuk menggambarkan grafik SPLDV, gunakan paling sedikit dua titik seperti pada tabel berikut.

Tentukan nilai y untuk x = 0.
2x + y = 4
⇔2( 0) + y = 4
⇔y = 4

Tentukan nilai x untuk y = 0.
2x + y = 4
⇔ 2x + 0 = 4
⇔ 2x = 4
⇔ x = 2

Tuliskan hasil yang diperoleh ke dalam tabel.

Ini berarti, titik yang diperoleh adalah A (0, 4) dan B (2, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

2. Tentukan penyeselesaian dari SPLDV:

2x + y = 6
2x + 4y = 12

Penyelesaian:

Langkah 1: gambarkan grafik untuk persamaan pertama.

Gunakan paling sedikit dua titik seperti pada tabel berikut.

Tentukan nilai y untuk x = 0.
2x + y = 6
⇔ 2(0) + y = 6
⇔ y = 6

Tentukan nilai x untuk y = 0.
2x + y = 6
⇔2x + 0 = 6
⇔2x = 6
⇔x = 3

Tuliskan hasil yang diperoleh ke dalam tabel.

Ini berarti, titik yang diperoleh adalah A (0, 6) dan B (3, 0).

Gambarkan titik tersebut ke dalam diagram Cartesius, kemudian hubungkan dengan sebuah garis lurus, sehingga terbentuk gambar di bawah ini.

2. Metode Eliminasi

Metode ini bertujuan untuk mengeliminasi salah satu variabel untuk mengetahui nilai variabel lainnya.

Contoh:

1. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan 2x+y=7 dan x−y=8 dengan metode eliminasi!

Pembahasan:
2x+y=7 . . . . (1)
x−y=8 . . . . (2)

Eliminasi suku variabel x: samakan koefisien x dengan mengalikan persamaan (1) dengan 1 dan dengan mengalikan persamaan 2 dengan 2, kemudian kurangkan.
2x+y=7x−y=8  |×1×2 |

   2x+y=72x−2y=16   −_
3y=−9
y=−3

Eliminasi suku variabel y: koefisien y pada persamaan (1) dan (2) hanya berbeda tanda, tidak perlu disamakan. Cukup hanya dengan menjumlahkan kedua persamaan.

   2x+y=7x−y=8   +_
3x=15
x=5

HP={(5,−3)}

2. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan 

$3x-4y=5$ dan $2x+3y=-8$ dengan cara atau metode eliminasi!

Pembahasan:
$3x-4y=5$ . . . . (1)
$2x+3y=-8$ . . . . (2)

Eliminasi suku variabel $x$: kalikan persamaan (1) dengan 2 dan kalikan persamaan (2) dengan 3, kemudian kurangkan.

$\begin{array}{c}3x-4y=5\\ 2x+3y=-8\end{array}|\begin{array}{c}\times 2\\ \times 3\end{array}|$

$\underset{-}{{\begin{array}{c}6x-8y=10\\ 6x+9y=-24\end{array}}_{-}}$
$-17y=34$
$y=-2$

Eliminasi suku variabel $y$: kalikan persamaan (1) dengan 3 dan kalikan persamaan (2) dengan 4. Karena koefisien $y$ pada persamaan (1) dan (2) hanya berbeda tanda, lakukan penjumlahan.

$\begin{array}{c}3x-4y=5\\ 2x+3y=-8\end{array}|\begin{array}{c}\times 3\\ \times 4\end{array}|$

$\underset{-}{{\begin{array}{c}9x-12y=15\\ 8x+12y=-32\end{array}}_{+}}$
$17x=-17$
$x=-1$

$HP=\left\{\right(-1,-2\left)\right\}$

3. Metode Subtitusi

Metode substitusi bertujuan untuk mengganti nilai suatu variabel di suatu persamaan dari persamaan lainnya.

Contoh:

1. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan x=2 dan 3x+2y=12 dengan metode substitusi!

Pembahasan:
Nilai dari x sudah diketahui, tinggal memasukkan nilai x=2 ke dalam persamaan 3x+2y=12.
3x+2y=12
3.2+2y=12
6+2y=12
2y=12−6
2y=6
y=3

HP={(2,3)}

2. Tentukanlah himpunan penyelesaian (HP) dari sistem persamaan $y=x+5$ dan $3x-y=7$ dengan metode substitusi!

Pembahasan:
$y=x+5$ . . . . (*)
$3x-y=7$ . . . . (**)

Persamaan (*) sudah dalam bentuk eksplisit, dengan begitu bisa langsung disubstitusikan ke dalam persamaan (**).
$3x-y=7$
$3x-(x+5)=7$ → jangan lupa tanda kurung.
$3x-x-5=7$
$2x=7+5$
$2x=12$
$x=6$

Substitusikan nilai $x=6$ kedalam persamaan (*) atau persamaan (**) untuk mendapatkan nilai dari $y$. Dalam hal ini kita ambil persamaan (*).
$y=x+5$
$y=6+5$
$y=11$

$HP=\left\{\right(6,11\left)\right\}$

4. Metode Gabungan

Metode ini merupakan gabungan dari metode eliminasi dan substitusi. Caranya, kamu dapat menggunakan metode eliminasi untuk mencari nilai x terlebih dahulu, kemudian ganti variabel x dengan nilai x yang sudah diperoleh dengan menggunakan metode substitusi untuk memperoleh nilai y.

Contoh:

1. Diketahui persamaan  x + 3y = 15 dan 3x + 6y = 30, dengan menggunakan metode campuran tentukanlah Himpunan penyelesaiannya !

Penyelesaian :

Diketahui :

Persamaan 1 = x + 3y = 15

Persamaan 2 = 3x + 6y = 30

Langkah Pertama Menggunakan Metode Eliminasi :

x + 3y = 15  | x3| <=> 3x +9x = 45

3x + 6y = 30  | x1| <=> 3x + 6y = 30    _

                                            0 + 3y = 15

                                              y = 5

Langkah Kedua Menggunakan Metode Substusi :

x + 3y = 15
x + 3.5 = 15
x + 15 = 15
x = 0

Jadi himpunan penyelesaian dari soal diatas adalah HP ={ 0 , 5 }